回溯三问：
当前操作是什么?
子问题是什么?
下一个子问题是什么?

1合唱团

描述
有 n 个学生站成一排，每个学生有一个能力值，牛牛想从这 n 个学生中按照顺序选取 k 名学生，要求相邻两个学生的位置编号的差不超过 d，使得这 k 个学生的能力值的乘积最大，你能返回最大的乘积吗？

输入描述：
每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1 <= n <= 50)，表示学生的个数，接下来的一行，包含 n 个整数，按顺序表示每个学生的能力值 ai（-50 <= ai <= 50）。接下来的一行包含两个整数，k 和 d (1 <= k <= 10, 1 <= d <= 50)。

输出描述：
输出一行表示最大的乘积。

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n;
    cin>>n;
    vector<int> arr(n);
    for(int i=0;i<n;i++) cin>>arr[i];
    int k,d;
    cin>>k>>d;

    vector<vector<long long>> result_max(n,vector<long long>(k+1,-0x3f));
    vector<vector<long long>> result_min(n,vector<long long>(k+1,0x3f));
    for(int i=0;i<n;i++){
        result_max[i][1]=arr[i];
        result_min[i][1]=arr[i];
    }

    for(int i=0;i<n;i++){
        for(int j=2;j<=k;j++){
            for(int m=1;m<=d&&(i-m)>=0;m++){
                result_max[i][j]=max(result_max[i][j],max(result_max[i-m][j-1]*arr[i],result_min[i-m][j-1]*arr[i]));
                result_min[i][j]=min(result_min[i][j],min(result_min[i-m][j-1]*arr[i],result_max[i-m][j-1]*arr[i]));
            }
        }
    }
    long long ans=-0x3f;
    for(int i=0;i<n;i++){
        ans=max(ans,result_max[i][k]);
    }
    cout<<ans<<endl;
    return 0;
}

2全排列

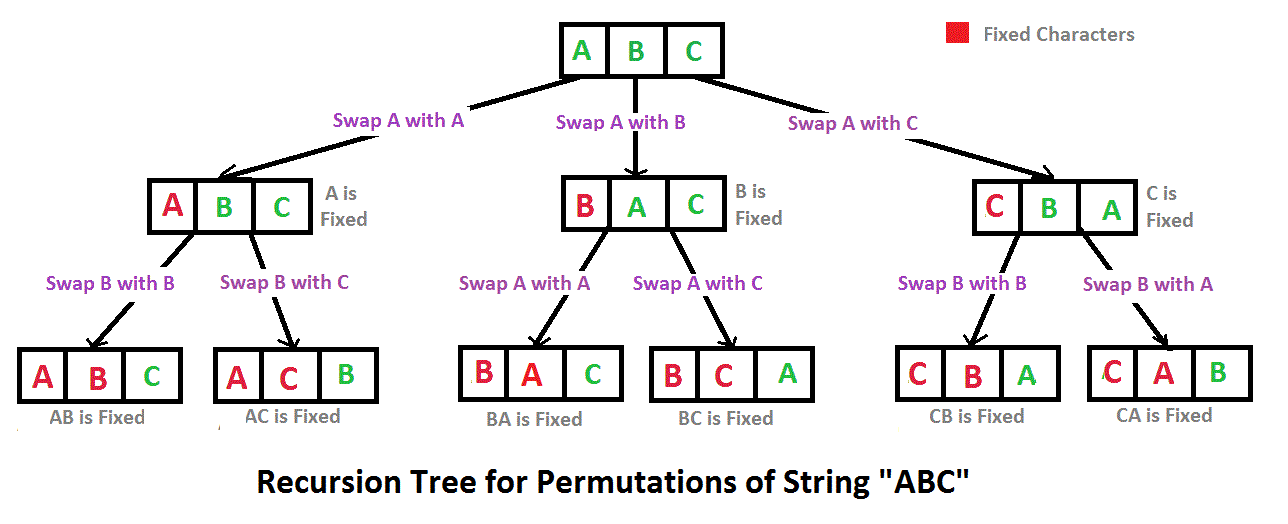
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

排列型回溯
解答：选哪个数 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<vector<int>> permute(vector<int> &nums) {
        int n = nums.size();
        vector<vector<int>> ans;
        vector<int> path(n), on_path(n);
        function<void(int)> dfs = [&](int i) {
            if (i == n) {
                ans.emplace_back(path);
                return;
            }
            for (int j = 0; j < n; j++) {
                if (!on_path[j]) {
                    path[i] = nums[j];
                    on_path[j] = true;
                    dfs(i + 1);
                    on_path[j] = false;
                }
            }
        };
        dfs(0);
        return ans;
    }
};

进阶版 - 包含重复元素

3全排列Ⅱ

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

思路：先排序 使重复的元素相邻 添加判断条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        vector<vector<int>> ans;
        vector<int> path(n), on_path(n); // 记录是否被选

        function<void(int)> dfs = [&](int i) {
            if (i == n) {
                ans.push_back(path);
                return;
            }
            for (int j = 0; j < n; j++) {
                if (on_path[j] ||
                    j > 0 && nums[j] == nums[j - 1] && !on_path[j - 1]) {
                    continue;
                }
                path[i] = nums[j];
                on_path[j] = true;
                dfs(i + 1);
                on_path[j] = false;
            }
        };
        dfs(0);
        return ans;
    }
};

相同类型题目

4字符串的排列

描述
输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。

例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

数据范围： n<10
要求：空间复杂度 O(n!)，时间复杂度 O(n!)

输入描述：
输入一个字符串,长度不超过10,字符只包括大小写字母。

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<string> Permutation(string str) {
        // write code here
        sort(str.begin(),str.end());
        int n=str.length();
        vector<string> ans;
        string path(n,0);
        vector<bool> on_path(n);//记录是否被选中

        function<void(int)> dfs=[&](int i){
            if(i==n){
                ans.push_back(path);
                return ;
            }
            for(int j=0;j<n;j++){
                if(on_path[j]||j>0&&str[j-1]==str[j]&&!on_path[j-1]) continue;
                on_path[j]=true;
                path[i]=str[j];
                dfs(i+1);
                on_path[j]=false;
            }
        };
        dfs(0);
        return ans;
    }
};

子集型回溯 - 考虑元素顺序

5子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的
子集 （幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

注意：由于[1,2] [2,1]是重复的，所以需要规定一个顺序

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        int n=nums.size();
        vector<vector<int>> ans;
        vector<int> path;
        function<void(int)> dfs=[&](int i){
            ans.push_back(path);
            for(int j=i;j<n;j++){
                path.push_back(nums[j]);
                dfs(j+1);
                path.pop_back();
            }
        };
        dfs(0);
        return ans;
    }
};

进阶版 - 包含重复元素

6子集Ⅱ

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的
子集 （幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

思路：排序 添加判断条件

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        vector<vector<int>> ans;
        vector<int> path;
        vector<bool> on_path(n,false);
        function<void(int)> dfs=[&](int i){
            ans.push_back(path);
            for(int j=i;j<n;j++){
                if(on_path[j]||j>0&&nums[j-1]==nums[j]&&!on_path[j-1]) continue;
                on_path[j]=true;
                path.push_back(nums[j]);
                dfs(j+1);
                path.pop_back();
                on_path[j]=false;
            }
        };
        dfs(0);
        return ans;
    }
};

7蘑菇阵

描述
现在有两个好友A和B，住在一片长有蘑菇的由n＊m个方格组成的草地，A在(1,1),B在(n,m)。现在A想要拜访B，
由于她只想去B的家，所以每次她只会走(i,j+1)或(i+1,j)这样的路线，
在草地上有k个蘑菇种在格子里(多个蘑菇可能在同一方格),问：A如果每一步随机选择的话(若她在边界上，则只有一种选择)，
那么她不碰到蘑菇走到B的家的概率是多少？

输入描述：
第一行N，M，K(1 ≤ N,M ≤ 20, k ≤ 100),N,M为草地大小，接下来K行，每行两个整数x，y，代表(x,y)处有一个蘑菇。

输出描述：
输出一行，代表所求概率(保留到2位小数)

思路：
假设P(i, j)表示从起点到(i, j)不踩到蘑菇的概率，那么该位置一定是从(i-1, j)或者(i, j-1)出走过来的。
而从(i-1, j)或者(i, j-1)到达(i, j)的概率是不等的，
比如：如果i或者j在边界，只能向一个方向移 动，此时走到(i, j)位置的概率为1，
当i或者j不在边界时，走到(i,j)的概率分别为0.5，
因此可得 出： P(i,j) = P(i-1, j) * (i==M? 1 : 0.5)+ P(i, j-1) * (j==N? 1 : 0.5)
需要注意这里的下标是从1开始的 打印要求两位小数

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n, m, k;
    while (cin >> n >> m >> k) {
        vector<vector<int>> map(n + 1, vector<int>(m + 1, 0));
        for (int i = 0; i < k; i++) {
            int row, col;
            cin >> row >> col;
            map[row][col] = 1;
        }

        vector<vector<double>> dp(n + 1, vector<double>(m + 1));
        dp[1][1] = 1.0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (!(i == 1 && j == 1)) {
                    dp[i][j] = dp[i - 1][j] * (j == m ? 1 : 0.5) + dp[i][j - 1] *
                                                                   (i == n ? 1 : 0.5);
                }
                if (map[i][j]) {
                    dp[i][j] = 0.0;
                }
            }
        }
        printf("%.2f\n", dp[n][m]);
    }
    return 0;
}

8电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    string MAP[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
    vector<string> letterCombinations(string digits) {
        int n=digits.length();
        if(n==0) return {};
        vector<string> ans;
        string path(n,0);
        function<void(int)> dfs=[&](int i){
            if(i==n){
                ans.push_back(path);
                return ;
            }
            for(char c:MAP[digits[i]-'0']){
                path[i]=c;
                dfs(i+1);
            }
        };
        dfs(0);
        return ans;
    }
};

9组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

相当于是规定长度的子集型回溯
采取倒叙枚举 当 i<d时此时枚举的长度一定不满足条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> ans;
        vector<int> path;
        function<void(int)> dfs=[&](int i){
            int d=k-path.size();
            if(d==0){
                ans.push_back(path);
                return ;
            }
            for(int j=i;j>=d;j--){
                path.push_back(j);
                dfs(j-1);
                path.pop_back();
            }
        };
        dfs(n);
        return ans;
    }
};

10组合总和Ⅲ

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

思路：
和上面类似倒叙枚举
比如i=5 d=3 如果 t>5+4+3-> t>(i+i-d+1)d/2=(2i-d+1)*d/2
条件不成立

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<vector<int>> ans;
        vector<int> path;
        function<void(int,int)> dfs=[&](int i,int t){
            int d=k-path.size();
            //剪枝
            if(t<0||t>(2*i-d+1)*d/2) return ;
            if(d==0){
                ans.push_back(path);
                return ;
            }
            for(int j=i;j>=d;j--){
                path.push_back(j);
                dfs(j-1,t-j);
                path.pop_back();
            }
        };
        dfs(9,n);
        return ans;
    }
};

11求和

描述

输入两个整数 n 和 m，从数列1，2，3…….n 中随意取几个数,使其和等于 m ,要求将其中所有的可能组合列出来

输入描述：

每个测试输入包含2个整数,n和m

输出描述：

按每个组合的字典序排列输出,每行输出一种组合

需要注意的是，这里要去按照字典序排列输出，与上述有所区别，从前往后遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <functional>
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n,m;
    cin>>n>>m;
    vector<vector<int>> ans;
    vector<int> path;
    function<void(int,int)> dfs=[&](int i,int t){
        if(t<0) return ;
        if(t==0){
            ans.push_back(path);
            return ;
        }
        for(int j=i;j<=n;j++){
            path.push_back(j);
            dfs(j+1,t-j);
            path.pop_back();
        }
    };
    dfs(1,m);
    for(auto v:ans){
        for(auto x:v){
            cout<<x<<" ";
        }
        cout<<endl;
    }
    return 0;
}

12马戏团

描述

搜狐员工小王最近利用假期在外地旅游，在某个小镇碰到一个马戏团表演，精彩的表演结束后发现团长正和大伙在帐篷前激烈讨论，
小王打听了下了解到， 马戏团正打算出一个新节目“最高罗汉塔”，即马戏团员叠罗汉表演。考虑到安全因素，要求叠罗汉过程中，
站在某个人肩上的人应该既比自己矮又比自己瘦，或相等。 团长想要本次节目中的罗汉塔叠的最高，由于人数众多，正在头疼如何安排人员的问题。
小王觉得这个问题很简单，于是统计了参与最高罗汉塔表演的所有团员的身高体重，并且很快找到叠最高罗汉塔的人员序列。
现在你手上也拿到了这样一份身高体重表，请找出可以叠出的最高罗汉塔的高度，这份表中马戏团员依次编号为1到N。

输入描述：

首先一个正整数N，表示人员个数。 之后N行，每行三个数，分别对应马戏团员编号，体重和身高。

输出描述：

正整数m，表示罗汉塔的高度。

体重不等时 需要体重小的 身高低的或者相等的
体重相等时 身高必须相等
为避免体重相等时 身高更高的被选中 采取体重升序排列 体重相等时 身高降序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Person {
    int id, weight, height;
    bool operator<(const Person& p) {
        if (weight != p.weight) {
            return weight <= p.weight;
        } else {
            return height > p.height;
        }
    }
};
int main() {
    int n;
    while (cin >> n) {
        vector<Person> arr(n);
        for (int i = 0; i < n; i++) {
            cin >> arr[i].id >> arr[i].weight >> arr[i].height;
        }
        sort(arr.begin(), arr.end());
        vector<int> dp(n, 1);
        int ans = 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (arr[j].height <= arr[i].height) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
                ans = max(ans, dp[i]);
            }
        }
        cout << ans << endl;
    }
    return 0;
}

13年终奖

描述

小东所在公司要发年终奖，而小东恰好获得了最高福利，他要在公司年会上参与一个抽奖游戏，
游戏在一个66的棋盘上进行，上面放着36个价值不等的礼物，每个小的棋盘上面放置着一个礼物，
他需要从左上角开始游戏，每次只能向下或者向右移动一步，到达右下角停止，
一路上的格子里的礼物小东都能拿到，请设计一个算法使小东拿到价值最高的礼物。
给定一个66的矩阵board，其中每个元素为对应格子的礼物价值,左上角为[0,0],请返回能获得的最大价值，
保证每个礼物价值大于100小于1000。

类似不同路径问题

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Bonus {
public:
    int getMost(vector<vector<int> > board) {
        // write code here
        int n=board.size();
        vector<vector<int>> memo(n,vector<int>(n,-1));
        function<int(int,int)> dfs=[&](int i,int j)->int{
            if(i<0||j<0) return 0;
            int& res=memo[i][j];
            if(res!=-1) return res;
            return res=max(dfs(i-1,j),dfs(i,j-1))+board[i][j];
        };
        return dfs(n-1,n-1);
    }
};

14完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，
其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,n);
        dp[0]=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j*j<=i;j++){
                dp[i]=min(dp[i],dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};

15走方格的方案数

描述

请计算n*m的棋盘格子（n为横向的格子数，m为竖向的格子数）从棋盘左上角出发沿着边缘线从左上角走到右下角，
总共有多少种走法，要求不能走回头路，即：只能往右和往下走，不能往左和往上走。

注：沿棋盘格之间的边缘线行走

数据范围： 1≤n,m≤8

输入描述：

输入两个正整数n和m，用空格隔开。(1≤n,m≤8)

输出描述：

输出一行结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <vector>
#include <functional>
using namespace std;

int main() {
    int n,m;
    cin>>n>>m;
    vector<vector<int>> memo(n+1,vector<int>(m+1,-1));
    function<int(int,int)> dfs=[&](int i,int j)->int{
        if(i<0||j<0) return 0;
        if(i==0&&j==0) return 1;
        int& res=memo[i][j];
        if(res!=-1) return res;
        return res=dfs(i-1,j)+dfs(i,j-1);
    };
    cout<<dfs(n,m)<<endl;
    return 0;
}

16跳石板

描述

小易来到了一条石板路前，每块石板上从1挨着编号为：1、2、3…….
这条石板路要根据特殊的规则才能前进：对于小易当前所在的编号为K的石板，
小易单次只能往前跳K的一个约数(不含1和K)步，即跳到K+X(X为K的一个非1和本身的约数)的位置。
小易当前处在编号为N的石板，他想跳到编号恰好为M的石板去，小易想知道最少需要跳跃几次可以到达。

例如：
N = 4，M = 24：
4->6->8->12->18->24
于是小易最少需要跳跃5次，就可以从4号石板跳到24号石板

输入描述：

输入为一行，有两个整数N，M，以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000)
输出描述：

输出小易最少需要跳跃的步数,如果不能到达输出-1

17不要二

描述

二货小易有一个W*H的网格盒子，网格的行编号为0H-1，网格的列编号为0W-1。
每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根
小易想知道最多可以放多少块蛋糕在网格盒子里。

输入描述：

每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)

输出描述：

输出一个最多可以放的蛋糕数

思想：
1+3=4
3+1=4
2+2=4
0+4=4
4+0=4

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int w,h;
    cin>>w>>h;
    int count=0;
    vector<vector<int>> dp(w,vector<int>(h,1));
    for(int i=0;i<w;i++)
    {
        for(int j=0;j<h;j++){
            if(dp[i][j]==1){
                count++;
                if(i+2<w){
                    dp[i+2][j]=0;
                }
                if(j+2<h){
                    dp[i][j+2]=0;
                }
            }
        }
    }
    cout<<count<<endl;
    return 0;
}

18宵暗的妖怪

题目描述
露米娅作为宵暗的妖怪，非常喜欢吞噬黑暗。 这天，她来到了一条路上，准备吞噬这条路上的黑暗。
这条道路一共被分为 n 部分，每个部分上的黑暗数量为 ai。
露米娅每次可以任取连续的未被吞噬过的 三部分，将其中的黑暗全部吞噬，并获得中间部分的饱食度。
露米娅想知道，自己能获得的饱食度最大值是多少？

输入描述:

1
2
3
4
5
第一行一个正整数 n ，代表道路被分的份数。
第二行有 n 个正整数 ai
，代表每一部分黑暗数量。
数据范围：
3≤n≤100000,1≤ai≤10^9

输出描述:

1
一个正整数，代表最终饱食度的最大值。

思路:
该元素是否被吞噬:没有被吞噬 选择前一个状态
被吞噬 选择上一个被吞噬的状态

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <vector>
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    vector<long long> v(n + 1);
    vector<long long> dp(n + 1);
    for (int i = 1; i <= n; i++)
    {
        cin >> v[i];
        if (i >= 3)
        {
            dp[i] = max(dp[i - 3] + v[i - 1], dp[i - 1]);
        }
    }
    cout << dp[n] << endl;
    return 0;
}

19取金币

描述

给定一个长度为 n 的正整数数组 coins，每个元素表示对应位置的金币数量。
取位置 i 的金币时，假设左边一堆金币数量是 L，右边一堆金币数量为 R，则获得
L∗cost[i]∗R的积分。如果左边或右边没有金币，则金币数量视为1。
请你计算最多能得到多少积分。
数据范围：数组长度满足 1≤n≤100 ，数组中的元素满足 1≤coinsi ≤100

解答

  1. 定义状态：
    • 设 dp[i][j] 表示从第 i 到第 j 的金币数组中，能获得的最大积分。
  2. 状态转移方程：
    对于区间 [i, j]，可以选择区间内的任意一个位置 k 作为最后取的位置。其获得的积分为:L * coins[k] * R
    其中 L 为左边的金币数，R 为右边的金币数，L 和 R 都取决于当前的区间边界。
    因此状态转移方程为:dp[i][j] = max(dp[i][j], dp[i][k-1] + dp[k+1][j] + L * coins[k] * R)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
  public:
    int getCoins(vector<int>& coins) {
        // write code here
        int n = coins.size();
        // 在数组两端加上虚拟的 1
        coins.insert(coins.begin(), 1);
        coins.push_back(1);
        // 创建 dp 数组，初始化为 0
        vector<vector<int>> dp(n + 2, vector<int>(n + 2, 0));
        // 动态规划，从较小的区间长度开始
        for (int len = 1; len <= n; ++len) {
            //枚举左边界
            for (int i = 1; i <= n - len + 1; ++i) {
                //计算右边界
                int j = i + len - 1;
                // 在 i 到 j 之间选择最后一个取的金币
                for (int k = i; k <= j; ++k) {
                    dp[i][j] = max(dp[i][j],
                                   dp[i][k - 1] + coins[i - 1] * coins[k] * coins[j + 1] + dp[k + 1][j]);
                }
            }
        }
        // 返回从第 1 个金币到第 n 个金币之间的最大积分
        return dp[1][n];
    }
};

20N皇后

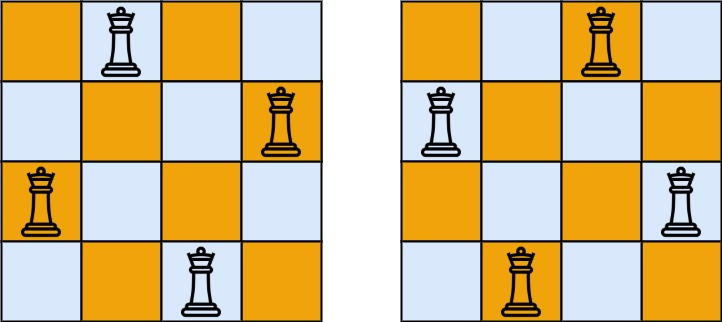
按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

实例

解答
使用 col 数组记录该行皇后所在位置 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> ans;
        vector<int> col(n),on_path(n),diag1(n*2-1),diag2(n*2-1);
        function<void(int)> dfs=[&](int r){
            if(r==n){
                vector<string> board(n);
                for(int i=0;i<n;i++){
                    board[i]=string(col[i],'.')+'Q'+string(n-1-col[i],'.');
                }
                ans.push_back(board);
                return ;
            }

            for(int c=0;c<n;c++){
                int rc=r-c+n-1;
                if(!on_path[c]&&!diag1[r+c]&&!diag2[rc]){
                    col[r]=c;
                    on_path[c]=diag1[r+c]=diag2[rc]=true;
                    dfs(r+1);
                    on_path[c]=diag1[r+c]=diag2[rc]=false;
                }
            }
        };
        dfs(0);
        return ans;
    }
};

21组合总和

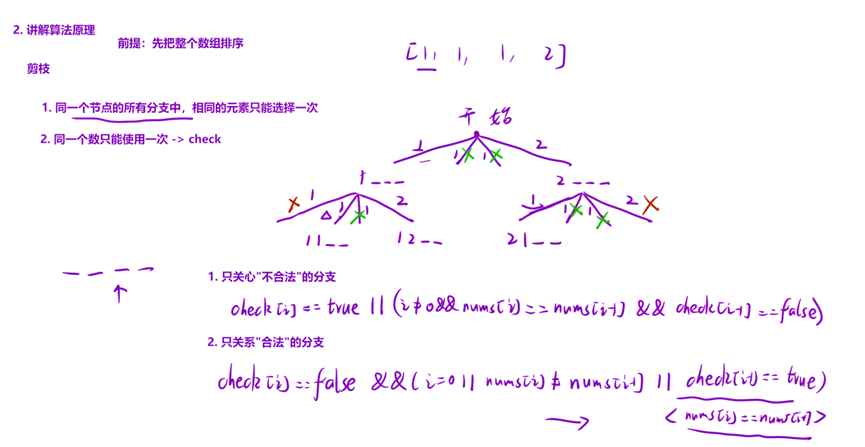
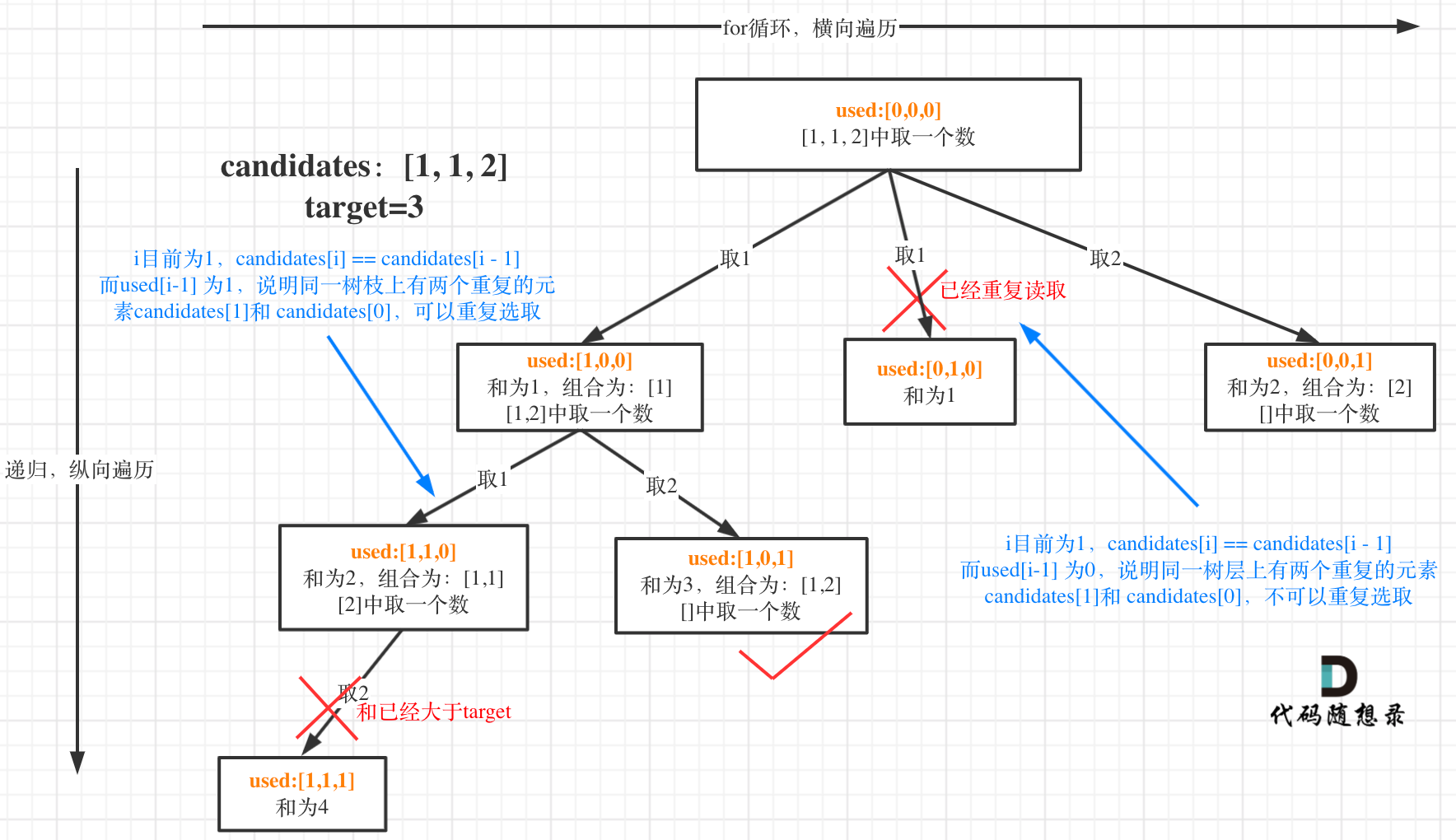
给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

先排序

图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    void backtracking(vector<int>& candidates,int target,int sum,int index,vector<bool>& visited){
        if(target==sum){
            ans.push_back(path);
            return ;
        }
        for(int i=index;i<candidates.size()&&sum+candidates[i]<=target;i++){
            if(i>0&&candidates[i-1]==candidates[i]&&!visited[i-1]) continue;
            sum+=candidates[i];
            path.push_back(candidates[i]);
            visited[i]=true;
            backtracking(candidates,target,sum,i+1,visited);
            visited[i]=false;
            path.pop_back();
            sum-=candidates[i];
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> visited(candidates.size(),0);
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,0,visited);
        return ans;
    }
};