描述
只由1-9组成,并且每个数只出现一次,如13,23,1289。
位数从高到低为递减或递增,如2459,87631。
请你判断一下,这个素数的回文数是否为素数(13的回文数是131,127的回文数是12721)。
输入描述:
输出描述:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <iostream> #include <algorithm> using namespace std;bool isPrime (long long num) if (num<2 ) return false ; for (long long i=2 ;i*i<=num;i++){ if (num%i==0 ) return false ; } return true ; } int main () string t; cin>>t; string tmp=t; reverse (tmp.begin (),tmp.end ()); tmp.erase (tmp.begin ()); t+=tmp; long long ret=atol (t.c_str ()); if (isPrime (ret)) { cout<<"prime" <<endl; }else { cout<<"noprime" <<endl; } return 0 ; }
描述
输入描述:
输出描述:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <iostream> #include <vector> #include <algorithm> using namespace std;struct Activity { int start; int end; }; bool compare (Activity a,Activity b) return a.end<b.end; } int main () int n; cin>>n; vector<Activity> arr (n) ; for (int i=0 ;i<n;i++){ cin>>arr[i].start>>arr[i].end; } sort (arr.begin (),arr.end (),compare); int count=1 ; int prevEnd=arr[0 ].end; for (int i=1 ;i<n;i++){ if (arr[i].start>=prevEnd){ count++; prevEnd=arr[i].end; } } cout<<count<<endl; return 0 ; }
描述
在地下室里放着n种颜色的手套,手套分左右手,但是每种颜色的左右手手套个数不一定相同。A先生现在要出门,
测试样例:
1 返回:10(解释:可以左手手套取2只,右手手套取8只)
思路:
如果某个颜色没有手套,就必须得把该颜色对应的另一边手套累加起来。
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Gloves { public : int findMinimum (int n, vector<int > left, vector<int > right) int leftsum = 0 , leftmin = INT_MAX, rightsum = 0 , rightmin = INT_MAX; int ans = 0 ; for (int i = 0 ; i < n; i++) { if (left[i] == 0 || right[i] == 0 ) { ans += left[i] + right[i]; } else { leftsum += left[i]; leftmin = min (leftmin, left[i]); rightsum += right[i]; rightmin = min (rightmin, right[i]); } } ans += min (leftsum - leftmin + 1 , rightsum - rightmin + 1 ) + 1 ; return ans; } };
居然有假币! 现在猪肉涨了,但是农民的工资却不见涨啊,没钱怎么买猪肉啊。nowcoder这就去买猪肉,
输入描述:
输出描述:
思路:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <iostream> using namespace std;int main () long long n; while (cin>>n){ int count=0 ; if (n==0 ){ break ; } while (n>=2 ){ if (n%3 ){ n=n/3 +1 ; count++; }else { n/=3 ; count++; } } cout<<count<<endl; } return 0 ; }
根据 逆波兰表示法,求该后缀表达式的计算结果。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
经典后序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution {public : bool isNumber (string ch) return !(ch=="+" ||ch=="-" ||ch=="*" ||ch=="/" ); } int evalRPN (vector<string>& tokens) stack<int > st; int n=tokens.size (); for (int i=0 ;i<n;i++){ string tmp=tokens[i]; if (isNumber (tmp)){ st.push (atoi (tmp.c_str ())); }else { int num2=st.top (); st.pop (); int num1=st.top (); st.pop (); switch (tmp[0 ]){ case '+' : st.push (num1+num2); break ; case '-' : st.push (num1-num2); break ; case '*' : st.push (num1*num2); break ; case '/' : st.push (num1/num2); break ; } } } return st.top (); } };
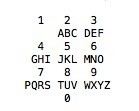
描述
上图是一个电话的九宫格,如你所见一个数字对应一些字母,因此在国外企业喜欢把电话号码设计成与自己公司名字相对应。
输入描述:
输出描述:
注意去重
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <cctype> #include <iostream> #include <set> #include <unordered_map> #include <vector> using namespace std;int main () string alpha="ABCDEFGHIJKLMNOPQRSTUVWXYZ" ; string num= "22233344455566677778889999" ; unordered_map<char , char > map; for (int i=0 ;i<26 ;i++){ map[alpha[i]]=num[i]; } set<string> set; int n; while (cin>>n){ set.clear (); for (int i=0 ;i<n;i++){ string line; cin>>line; string ans; for (auto ch:line){ if (isdigit (ch)){ ans+=ch; }else if (isupper (ch)){ ans+=map[ch]; } } ans=ans.substr (0 ,3 )+"-" +ans.substr (3 ); set.insert (ans); } for (auto str:set){ cout<<str<<endl; } cout<<endl; } return 0 ; }
描述
定义一个单词的“兄弟单词”为:交换该单词字母顺序(注:可以交换任意次),而不添加、删除、修改原有的字母就能生成的单词。
数据范围: 1≤n≤1000 ,输入的字符串长度满足 1≤len(str)≤10 , 1≤k<n
输入描述:
输入只有一行。 先输入字典中单词的个数n,再输入n个单词作为字典单词。 然后输入一个单词x 最后后输入一个整数k
输出描述:
第一行输出查找到x的兄弟单词的个数m 第二行输出查找到的按照字典顺序排序后的第k个兄弟单词,没有符合第k个的话则不用输出。
将字典中的单词先放到 vector 中
将 vector 进行排序
isBrother 函数依次判定每个输入的单词是否是兄弟单词
判定兄弟单词的规则是 : 先判定长度;如果长度相同, 再看是否是完全相同(完全相同不算兄弟);然后将两个单词排序, 排序相同才是真兄弟单词.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <iostream> #include <vector> #include <algorithm> using namespace std;bool isBrother (string str1,string str2) if (str1==str2) return false ; if (str1.length ()!=str2.length ()) return false ; sort (str1.begin (),str1.end ()); sort (str2.begin (),str2.end ()); return str1==str2; } int main () int n; cin>>n; vector<string> arr (n) ; for (int i=0 ;i<n;i++) cin>>arr[i]; string dict; cin>>dict; int k; cin>>k; int count=0 ; string ans="" ; sort (arr.begin (),arr.end ()); for (int i=0 ;i<n;i++){ if (isBrother (arr[i], dict)){ count++; if (count==k){ ans=arr[i]; } } } cout<<count<<endl; if (count>=k){ cout<<ans<<endl; } return 0 ; }
模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 s += " " ; string temp = "" ; vector<string> res; for (char ch : s) { if (ch == ' ' ) { if (!temp.empty ()) { res.push_back (temp); temp.clear (); } } else temp += ch; }
2、没有前后置的空格不需要判断空串
1 2 3 4 5 6 7 8 9 10 11 12 13 s += " " ; string temp = "" ; vector<string> res; for (char ch : s) { if (ch == ' ' ) { res.push_back (temp); temp.clear (); } else temp += ch; }
描述
对字符串中的所有单词进行倒排。
说明:
构成单词的字符只有26个大写或小写英文字母;
非构成单词的字符均视为单词间隔符;
要求倒排后的单词间隔符以一个空格表示;如果原字符串中相邻单词间有多个间隔符时,倒排转换后也只允许出现一个空格间隔符;
每个单词最长20个字母;
数据范围:字符串长度满足 1≤n≤10000
输入描述:
输入一行,表示用来倒排的句子
输出描述:
输出句子的倒排结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <cctype> #include <iostream> #include <sstream> #include <vector> using namespace std;int main () string str; getline (cin,str); for (auto & ch:str){ if (!isalpha (ch)){ ch=' ' ; } } stringstream ss; ss<<str; vector<string> ans; while (ss>>str){ ans.push_back (str); } for (int i=ans.size ()-1 ;i>0 ;i--){ cout<<ans[i]<<" " ; } cout<<ans[0 ]<<endl; return 0 ; }
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
从左往右 从上往下 从右往左 从下往上
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : vector<int > spiralOrder (vector<vector<int >>& matrix) { if (matrix.size ()==0 ){ return {}; } int l=0 ,r=matrix[0 ].size ()-1 ,t=0 ,b=matrix.size ()-1 ; vector<int > ans; while (true ){ for (int i=l;i<=r;i++) ans.push_back (matrix[t][i]); if (++t>b) break ; for (int i=t;i<=b;i++) ans.push_back (matrix[i][r]); if (--r<l) break ; for (int i=r;i>=l;i--) ans.push_back (matrix[b][i]); if (--b<t) break ; for (int i=b;i>=t;i--) ans.push_back (matrix[i][l]); if (++l>r) break ; } return ans; } };
给定一个数组arr长度为N,你可以把任意长度大于0且小于N的前缀作为左部分,剩下的 作为右部分。
输入描述:
1 2 第一行输入一个整数N(N<100000) 第二行输入N个整数表示arr
输出描述:
1 输出左部分最大值减去右部分最大值的绝对值的最大值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <iostream> #include <vector> using namespace std;int main () int n; cin>>n; vector<int > arr (n) ; for (int i=0 ;i<n;i++) cin>>arr[i]; int ans=0 ; for (auto x:arr){ ans=max (ans,x); } cout<<(ans-min (arr[0 ],arr[n-1 ]))<<endl; return 0 ; }
NowCoder生活在充满危险和阴谋的年代。为了生存,他首次发明了密码,用于军队的消息传递。假设你是军团中的一名军官,需要把发送来的消息破译出来、并提
输入描述:
1 2 输入包括多组数据,每组数据一行,为收到的密文。 密文仅有空格和大写字母组成。
输出描述:
密码 > ‘E’
1 2 3 4 5 6 7 8 9 10 11 12 13 #include <iostream> using namespace std;int main () char c; while ((c = getchar ()) != EOF) { if ('A' <= c && 'Z' >= c) { c = (c > 'E' ) ? (c - 5 ) : (c + 21 ); } putchar (c); } return 0 ; }
题目描述
输入描述:
1 2 3 4 第一行一个正整数 𝑛 第二行 n 个正整数 𝑎𝑖 ,用空格隔开。 第三行一个正整数 q 。 接下来的 q 行,每行一个正整数 x ,代表一次询问。 数据范围:1≤q≤1e5,1≤ai≤1e9,2≤x≤n≤1e5
输出描述:
1 2 输出 𝑞 行,每行一个正整数,代表一次询问,输出前 x 个果冻中美味度第二大的值。
不采取排序的方式 如果数组过大 程序会超时
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #include <vector> #include <algorithm> using namespace std;int main () int n; cin >> n; vector<int > a (n + 1 ) ; vector<int > first_max (n + 1 ) , second_max (n + 1 ) ; for (int i = 1 ; i <= n; ++i) { cin >> a[i]; } for (int i = 1 ; i <= n; ++i) { if (a[i] > first_max[i - 1 ]) { second_max[i] = first_max[i - 1 ]; first_max[i] = a[i]; } else if (a[i] > second_max[i - 1 ]) { second_max[i] = a[i]; first_max[i] = first_max[i - 1 ]; } else { first_max[i] = first_max[i - 1 ]; second_max[i] = second_max[i - 1 ]; } } int q; cin >> q; while (q--) { int x; cin >> x; cout << second_max[x] << endl; } return 0 ; }
题目描述
读入一个
给出 q个操作,输出操作完的矩阵
输入描述:
1 2 3 4 第一行一个数n(1≤n≤1000),表示矩阵大小 接下来n行,每行n个数,描述矩阵,其中数字范围为[1,2000] 一下来一行一个数q(1≤q≤100000),表示询问次数 接下来q行,每行一个数x(x=1或x=2),描述每次询问
输出描述:
简单模拟即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 #include <iostream> #include <vector> using namespace std;void rotate180 (vector<vector<int >> &matrix, int n) for (int i = 0 ; i < n / 2 ; ++i) { for (int j = 0 ; j < n; ++j) { swap (matrix[i][j], matrix[n - 1 - i][n - 1 - j]); } } if (n % 2 != 0 ) { for (int j = 0 ; j < n / 2 ; ++j) { swap (matrix[n / 2 ][j], matrix[n / 2 ][n - 1 - j]); } } } void mirrorRows (vector<vector<int >> &matrix, int n) for (int i = 0 ; i < n / 2 ; ++i) { swap (matrix[i], matrix[n - 1 - i]); } } int main () int n; cin >> n; vector<vector<int >> matrix (n, vector <int >(n)); for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < n; ++j) { cin >> matrix[i][j]; } } int q; cin >> q; int rotate180_count = 0 , mirror_count = 0 ; while (q--) { int x; cin >> x; if (x == 1 ) { rotate180_count++; } else if (x == 2 ) { mirror_count++; } } if (rotate180_count % 2 == 1 ) { rotate180 (matrix, n); } if (mirror_count % 2 == 1 ) { mirrorRows (matrix, n); } for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < n; ++j) { cout << matrix[i][j] << " " ; } cout << endl; } return 0 ; }
一个正整数可以分解成一个或多个数组的积。例如36=22 3*3,即包含2和3两个因子。
输入描述:
1 2 输入包括多组数据。 每组数据仅有一个整数n (2≤n≤100000)。
输出描述:
思路:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <iostream> #include <math.h> using namespace std;int main () int n; while (cin>>n){ int k=0 ; for (int i=2 ;i<=sqrt (n);i++){ if (n%i==0 ){ while (n%i==0 ){ n/=i; } k++; } } if (n!=1 ) k++; cout<<k<<endl; } return 0 ; }
所谓因子分解,就是把给定的正整数a,分解成若干个素数的乘积,即 a = a1 × a2 × a3 × … × an,
输入描述:
1 输入包含多组数据,每组数据包含一个正整数a(2≤a≤1000000)。
输出描述:
1 对应每组数据,以“a = a1 * a2 * a3...”的形式输出因式分解后的结果。
简单素数判断
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> #include <vector> using namespace std;void primeFactorization (int n) cout << n << " = " ; bool first = true ; for (int i = 2 ; i * i <= n; ++i) { while (n % i == 0 ) { if (!first) { cout << " * " ; } cout << i; n /= i; first = false ; } } if (n > 1 ) { if (!first) { cout << " * " ; } cout << n; } cout << endl; } int main () int a; while (cin >> a) { primeFactorization (a); } return 0 ; }
描述
一块花布条,里面有些图案,另有一块直接可用的小饰条,里面也有一些图案。
输入描述:
输出描述:
对应每组输入,输出能从花纹布中剪出的最多小饰条个数,如果一块都没有,那就输出0,每个结果占一行。
字符查找 str.find
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <iostream> using namespace std;int countSubstrings (const string& s,const string& t) int count=0 ; size_t pos=0 ; while ((pos=s.find (t,pos))!=string::npos){ count++; pos+=t.length (); } return count; } int main () string s,t; while (cin>>s>>t){ cout<<countSubstrings (s,t)<<endl; } return 0 ; }
描述
NowCoder每天要给许多客户写电子邮件。正如你所知,如果一封邮件中包含多个收件人,
输入描述:
输入包含多组数据。
输出描述:
对应每一组输入,输出一行收件人列表。
字符串查找对应的字符
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <iostream> #include <string> using namespace std;int main () int n = 0 ; while (cin >> n) { string str; getchar (); for (int i = 0 ; i < n; i++) { getline (cin, str); if (str.find (' ' ) != str.npos || str.find (',' ) != str.npos) cout << '"' << str << '"' ; else cout << str; (i + 1 != n) ? cout << ", " : cout << endl; } } return 0 ; }
NowCoder每天要处理许多邮件,但他并不是在收件人列表中,有时候只是被抄送。
输入描述:
1 2 3 4 输入有多组数据,每组数据有两行。 第一行抄送列表,姓名之间用一个逗号隔开。如果姓名中包含空格或逗号, 则姓名包含在双引号里。总长度不超过512个字符。 第二行只包含一个姓名,是待查找的用户的名字(姓名要完全匹配)。长度不超过16个字符。
输出描述:
1 2 如果第二行的名字出现在收件人列表中,则输出“Ignore”,表示这封邮件不重要; 否则,输出“Important!”,表示这封邮件需要被优先处理。
截取字符串 substr
通过getiine(cin, names)方法获取第一行中的所有名字
解析出第一行中的所有名字保存在unordered_set中
获取第二行中的名字,检测该名字是否存在,并按照题目的要求进行输出
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <iostream> #include <unordered_set> using namespace std;int main () string name; while (getline (cin,name)){ unordered_set<string> set; size_t pos=0 ; while (pos<name.length ()){ if (name[pos]=='\"' ){ size_t end=name.find ('\"' ,pos+1 ); set.insert (name.substr (pos+1 ,end-pos-1 )); pos=end+2 ; }else { size_t end=name.find (',' ,pos); if (end==-1 ){ set.insert (name.substr (pos)); break ; } set.insert (name.substr (pos,end-pos)); pos=end+1 ; } } getline (cin,name); if (set.find (name)==set.end ()){ cout<<"Important!" <<endl; }else { cout<<"Ignore" <<endl; } } return 0 ; }
一只成熟的兔子每天能产下一胎兔子。每只小兔子的成熟期是一天。 某人领养了一只小兔子,请问第N天以后,他将会得到多少只兔子。
输入描述:
1 测试数据包括多组,每组一行,为整数n(1≤n≤90)。
输出描述:
1 对应输出第n天有几只兔子(假设没有兔子死亡现象)。
斐波那契数列
1 2 3 4 5 6 7 8 9 10 11 12 13 #include <iostream> using namespace std;int main () long long n[91 ] = { 1 , 2 }; for (int i = 2 ; i <= 90 ; i++) { n[i] = n[i - 1 ] + n[i - 2 ]; } int d; while (std::cin >> d) { printf ("%lld\n" , n[d - 1 ]); } }
描述
输入描述:
输入包含多组数据。
输出描述:
对应每一组数据,输出相应的、按照字典顺序排序的“mkdir -p”命令。
判断字符串是否相等,字串问题
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> #include <algorithm> #include <vector> using namespace std;int main () int n; while (cin>>n){ vector<string> path (n) ; for (int i=0 ;i<n;i++){ cin>>path[i]; } vector<bool > flag (n,true ) ; sort (path.begin (),path.end ()); for (int i=0 ;i<n-1 ;i++){ if (path[i]==path[i+1 ]){ flag[i]=false ; } if (path[i+1 ].length ()>path[i].length ()&&path[i+1 ].substr (0 ,path[i].length ())==path[i]&&path[i+1 ][path[i].length ()]=='/' ){ flag[i]=false ; } } for (int i=0 ;i<n;i++){ if (flag[i]){ cout<<"mkdir -p " <<path[i]<<endl; } } cout<<endl; } return 0 ; }
描述
找出字符串中第一个只出现一次的字符
输入描述:
输入一个非空字符串
输出描述:
输出第一个只出现一次的字符,如果不存在输出-1
注意是字符(256)而不是字母(26)
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> #include <unordered_map> using namespace std;char getFirstOneChar (string str) int hash[256 ]={0 }; for (auto ch : str) { hash[ch]++; } for (auto ch : str) { if (hash[ch] == 1 ) { return ch; } } return -1 ; } int main () string str; cin >> str; char res=getFirstOneChar (str); if (res==-1 ){ cout<<-1 <<endl; }else { cout<<res<<endl; } return 0 ; }
描述
春节期间小明使用微信收到很多个红包,非常开心。在查看领取红包记录时发现,某个红包金额出现的次数超过了红包总数的一半。
超过数组一半的元素->如果存在,一定在数组正中间
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Gift { public : int getValue (vector<int > gifts, int n) map<int , int > map; int middle = n / 2 ; for (auto x : gifts) { map[x]++; } for (auto x : map) { if (x.second > middle) { return x.first; } } return 0 ; } };
描述
老猴子辛苦了一辈子,给那群小猴子们留下了一笔巨大的财富——一大堆桃子。老猴子决定把这些桃子分给小猴子。
输入描述:
输入包括多组测试数据。
输出描述:
每组测试数据对应一行输出。
数学分析题:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> #include <math.h> using namespace std;int main () int n; while (cin>>n){ if (n==0 ) break ; long total=pow (5 ,n)-4 ; long left=pow (4 ,n)+n-4 ; cout<<total<<" " <<left<<endl; } return 0 ; }
对于一个小写字母而言,游游可以通过一次操作把这个字母变成相邻的字母。
输入描述:
1 一个仅包含小写字母,长度不超过100000的字符串。
输出描述:
思路:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <iostream> using namespace std;int main () string s; cin >> s; int cnt = 1e9 ; for (char i = 'a' ; i <= 'z' ; i++) { int sum = 0 ; for (int j = 0 ; j < s.size (); j++) { sum += min (abs (s[j] - i), 26 - abs (s[j] - i)); } cnt = min (cnt, sum); } cout << cnt; return 0 ; }
描述
N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学不交换位置就能排成合唱队形。
输入描述:
输入的第一行是一个整数N(2 <= N <= 100),表示同学的总数。 第一行有n个整数,用空格分隔,第i个整数Ti(130 <= Ti <= 230)是第i位同学的身高(厘米)。
输出描述:
可能包括多组测试数据,对于每组数据, 输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。
思考:
左侧递增子序列:计算每个位置 i,以该位置为结尾的最长递增子序列的长度。
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <iostream> #include <vector> #include <algorithm> using namespace std;int minStudentsToRemove (int N, const vector<int >& heights) vector<int > left (N, 1 ) ; vector<int > right (N, 1 ) ; for (int i = 1 ; i < N; ++i) { for (int j = 0 ; j < i; ++j) { if (heights[i] > heights[j]) { left[i] = max (left[i], left[j] + 1 ); } } } for (int i = N - 2 ; i >= 0 ; --i) { for (int j = N - 1 ; j > i; --j) { if (heights[i] > heights[j]) { right[i] = max (right[i], right[j] + 1 ); } } } int maxLength = 0 ; for (int i = 0 ; i < N; ++i) { maxLength = max (maxLength, left[i] + right[i] - 1 ); } return N - maxLength; } int main () int N; while (cin >> N) { vector<int > heights (N) ; for (int i = 0 ; i < N; ++i) { cin >> heights[i]; } cout << minStudentsToRemove (N, heights) << endl; } return 0 ; }
描述
给定两个int A和B。编写一个函数返回A+B的值,但不得使用+或其他算数运算符。
解答
1 2 3 4 5 6 7 8 9 10 11 class UnusualAdd {public : int addAB (int A, int B) if (A==0 ) return B; if (B==0 ) return A; int a=A^B; int b=(A&B)<<1 ; return addAB (a, b); } };
描述
给定一个二维数组board,代表棋盘,其中元素为1的代表是当前玩家的棋子,0表示没有棋子,-1代表是对方玩家的棋子。
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <iostream> using namespace std;#include <vector> class Board { public : bool checkWon (vector<vector<int >> board) int n=board.size (); bool winMainDiag=true ,winAntiDiag=true ; for (int i=0 ;i<n;i++){ bool winRow=true ,winCol=true ; for (int j=0 ;j<n;j++){ if (board[i][j]!=1 ) winRow=false ; if (board[j][i]!=1 ) winCol=false ; } if (winRow||winCol) return true ; if (board[i][i]!=1 ) winMainDiag=false ; if (board[i][n-i-1 ]!=1 ) winAntiDiag=false ; } return winMainDiag||winAntiDiag; }; };
描述
密码按如下规则进行计分,并根据不同的得分为密码进行安全等级划分。
一、密码长度:
二、字母:
三、数字:
四、符号:
五、奖励(只能选符合最多的那一种奖励):
最后的评分标准:
= 90: 非常安全
对应输出为:
VERY_SECURE
请根据输入的密码字符串,进行安全评定。
注:0x2F)0x40)0x60) (ASCII码:0x7B~0x7E)
提示:
输入描述:
输入一个string的密码
输出描述:
输出密码等级
判断是否是字符 ispunct
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 #include <iostream> #include <string> #include <ctype.h> using namespace std;int getLengthScore (const string& password) int len = password.length (); if (len <= 4 ) return 5 ; if (len <= 7 ) return 10 ; return 25 ; } int getLetterScore (const string& password) bool hasLower = false , hasUpper = false ; for (auto ch : password) { if (islower (ch)) hasLower = true ; if (isupper (ch)) hasUpper = true ; } if (hasLower && hasUpper) return 20 ; if (hasLower || hasUpper) return 10 ; return 0 ; } int getDigitScore (const string& password) int digitcount = 0 ; for (auto ch : password) { if (isdigit (ch)) digitcount++; } if (digitcount == 1 ) return 10 ; if (digitcount > 1 ) return 20 ; return 0 ; } int getSymbolScore (const string& password) int symbolcount = 0 ; for (auto ch : password) { if (ispunct (ch)) symbolcount++; } if (symbolcount == 1 ) return 10 ; if (symbolcount > 1 ) return 20 ; return 0 ; } int getBonusScore (const string& password) bool hasLower = false , hasUpper = false , hasDigit = false , hasSymbol = false ; for (char ch : password) { if (islower (ch)) hasLower = true ; if (isupper (ch)) hasUpper = true ; if (isdigit (ch)) hasDigit = true ; if (ispunct (ch)) hasSymbol = true ; } if (hasLower && hasUpper && hasDigit && hasSymbol) return 5 ; if ((hasLower || hasUpper) && hasDigit && hasSymbol) return 3 ; if ((hasLower || hasUpper) && hasDigit) return 2 ; return 0 ; } string getPasswordStrength (int score) { if (score >= 90 ) return "VERY_SECURE" ; if (score >= 80 ) return "SECURE" ; if (score >= 70 ) return "VERY_STRONG" ; if (score >= 60 ) return "STRONG" ; if (score >= 50 ) return "AVERAGE" ; if (score >= 25 ) return "WEAK" ; return "VERY_WEAK" ; } int main () string password; cin >> password; int score = 0 ; score += getLengthScore (password); score += getLetterScore (password); score += getDigitScore (password); score += getSymbolScore (password); score += getBonusScore (password); cout << getPasswordStrength (score) << endl; return 0 ; }
描述
求一个int类型数字对应的二进制数字中1的最大连续数,例如3的二进制为00000011,最大连续2个1
数据范围:数据组数: 1≤t≤5 , 1≤n≤500000
输入描述:
输入一个int类型数字
输出描述:
输出转成二进制之后连续1的个数
求一个二进制数有几个连续的1,用n与n<<1作&
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> using namespace std;int main () int n; cin>>n; int count=0 ; while (n){ n=n&(n<<1 ); count++; } cout<<count<<endl; return 0 ; }
求一个二进制数有几个1,用n与n-1作&
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> using namespace std;int main () int n; cin>>n; int count=0 ; while (n){ n=n&(n-1 ); count++; } cout<<count<<endl; return 0 ; }
描述
给定两个32位整数n和m,同时给定i和j,将m的二进制数位插入到n的二进制的第j到第i位,保证n的第j到第i位均为零,
测试样例:
解答
1 2 3 4 5 6 7 8 class BinInsert {public : int binInsert (int n, int m, int j, int i) m=m<<j; return n|m; } };
描述
任意一个偶数(大于2)都可以由2个素数组成,组成偶数的2个素数有很多种情况,本题目要求输出组成指定偶数的两个素数差值最小的素数对。
数据范围:输入的数据满足 4≤n≤1000
输入描述:
输入一个大于2的偶数
输出描述:
从小到大输出两个素数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <iostream> using namespace std;bool isPrime (int num) if (num<2 ) return false ; for (int i=2 ;i*i<=num;i++){ if (num%i==0 ) return false ; } return true ; } int main () int n; cin>>n; int half=n/2 ; int i=0 ; for (i=half;i>1 ;i--){ if (isPrime (i)&&isPrime (n-i)){ break ; } } cout<<i<<endl; cout<<n-i<<endl; return 0 ; }
描述
在命令行输入如下命令:
xcopy /s c:\ d:\e,
各个参数如下:
参数1:命令字xcopy
参数2:字符串/s
参数3:字符串c:\
参数4: 字符串d:\e
请编写一个参数解析程序,实现将命令行各个参数解析出来。
解析规则:
1.参数分隔符为空格
2.对于用””包含起来的参数,如果中间有空格,不能解析为多个参数。比如在命令行输入xcopy /s “C:\program files” “d:"时,参数仍然是4个,第3个参数应该是字符串C:\program files,而不是C:\program,注意输出参数时,需要将””去掉,引号不存在嵌套情况。
3.参数不定长
4.输入由用例保证,不会出现不符合要求的输入
数据范围:字符串长度: 1≤s≤1000
输入描述:
输入一行字符串,可以有空格
输出描述:
输出参数个数,分解后的参数,每个参数都独占一行
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <iostream> #include <vector> using namespace std;void cmdLineParse (const string& str) vector<string> param; string tmp="" ; bool flag=false ; for (auto ch:str){ if (ch=='"' ){ flag=!flag; }else if (ch==' ' &&!flag){ param.push_back (tmp); tmp.clear (); }else { tmp+=ch; } } if (!tmp.empty ()){ param.push_back (tmp); } cout<<param.size ()<<endl; for (auto s:param){ cout<<s<<endl; } } int main () string str; getline (cin,str); cmdLineParse (str); return 0 ; }
给出一个区间[a, b],计算区间内“神奇数”的个数。
输入描述:
1 输入为两个整数a和b,代表[a, b]区间 (1 ≤ a ≤ b ≤ 10000)。
输出描述:
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <iostream> #include <unordered_set> using namespace std;bool isPrime (int num) if (num<2 ) return false ; for (int i=2 ;i*i<=num;i++){ if (num%i==0 ) return false ; } return true ; } bool isMagicNumber (int num) string str=to_string (num); int len=str.length (); unordered_set<int > set; for (int i=0 ;i<len;i++){ for (int j=0 ;j<len;j++){ if (i!=j){ int num=(str[i]-'0' )*10 +(str[j]-'0' ); if (num>10 ){ set.insert (num); } } } } for (auto x:set){ if (isPrime (x)) return true ; } return false ; } int main () int a,b; cin>>a>>b; int count=0 ; for (int i=a;i<=b;i++){ if (isMagicNumber (i)) count++; } cout<<count<<endl; return 0 ; }
描述
给定一个十进制数M,以及需要转换的进制数N。将十进制数M转化为N进制数
输入描述:
输入为一行,M(32位整数)、N(2 ≤ N ≤ 16),以空格隔开。
输出描述:
为每个测试实例输出转换后的数,每个输出占一行。如果N大于9,则对应的数字规则参考16进制(比如,10用A表示,等等)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <iostream> #include <algorithm> using namespace std;int main () int M,N; cin>>M>>N; string str="0123456789ABCDEF" ; string ans="" ; bool flag=false ; if (M<0 ){ flag=true ; M=-M; }else if (M==0 ){ cout<<0 <<endl; return 0 ; } while (M){ ans+=str[M%N]; M/=N; } if (flag){ ans+='-' ; } reverse (ans.begin (),ans.end ()); cout<<ans<<endl; return 0 ; }
描述
Fibonacci数列是这样定义的:
输入描述:
输入为一个正整数N(1 ≤ N ≤ 1,000,000)
输出描述:
输出一个最小的步数变为Fibonacci数”
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <iostream> using namespace std;int main () int N,f0=0 ,f1=1 ,l=0 ,r=0 ; cin>>N; while (1 ){ int f=f0+f1; f0=f1; f1=f; if (f<N){ l=N-f; }else { r=f-N; break ; } } cout<< min (l,r) <<endl; return 0 ; }
描述
考拉有n个字符串字符串,任意两个字符串长度都是不同的。考拉最近学习到有两种字符串的排序方法:
1.根据字符串的字典序排序。例如:
2.根据字符串的长度排序。例如:
考拉想知道自己的这些字符串排列顺序是否满足这两种排序方法,考拉要忙着吃树叶,所以需要你来帮忙验证。
输入描述:
输入第一行为字符串个数n(n ≤ 100) 接下来的n行,每行一个字符串,字符串长度均小于100,均由小写字母组成
输出描述:
如果这些字符串是根据字典序排列而不是根据长度排列输出”lexicographically”,
思路:长度,字典序如何比较 lambda表达式
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <iostream> #include <vector> #include <algorithm> using namespace std;int main () int n; cin>>n; vector<string> arr (n) ; for (int i=0 ;i<n;i++){ cin>>arr[i]; } vector<string> arr_copy=arr; sort (arr.begin (),arr.end ()); bool lexicographically=true ; for (int i=0 ;i<n;i++){ if (arr[i]!=arr_copy[i]){ lexicographically=false ; break ; } } sort (arr.begin (),arr.end (),[](const string&str1,const string&str2){ return str1.length ()<str2.length (); }); bool lengths=true ; for (int i=0 ;i<n;i++){ if (arr[i]!=arr_copy[i]){ lengths=false ; break ; } } if (lexicographically&&lengths){ cout<<"both" <<endl; }else if (lexicographically&&!lengths){ cout<<"lexicographically" <<endl; }else if (!lexicographically&&lengths){ cout<<"lengths" <<endl; }else { cout<<"none" <<endl; } return 0 ; }
给定一个字符串 s ,检查是否能重新排布其中的字母,使得两相邻的字符不同。
返回 s 的任意可能的重新排列。若不可行,返回空字符串 “” 。
思路: m>n−m+1,那么无法重排,返回空字符串;从偶数下标开始填,如果单个字母出现的次数过多,则不能进行重构
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public : string reorganizeString (string s) { int n=s.length (); unordered_map<char ,int > mp; for (auto ch:s) mp[ch]++; vector<pair<char ,int >> v (mp.begin (),mp.end ()); sort (v.begin (),v.end (),[](const auto &p,const auto &q){ return p.second>q.second; }); int m=v[0 ].second; if (m>n-m+1 ){ return "" ; } string ans (n,0 ) ; int i=0 ; for (auto [ch,cnt]:v){ while (cnt--){ ans[i]=ch; i+=2 ; if (i>=n){ i=1 ; } } } return ans; } };
题目描述
mari每天都非常shiny。她的目标是把正能量传达到世界的每个角落!
输入描述:
1 2 第一行一个正整数n,代表字符串的长度。(1≤n≤300000) 第二行为一个长度为n,仅由小写字母组成的字符串。
输出描述:
需要注意数值的范围
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <iostream> using namespace std; int main () long long n; cin>>n; string str; cin>>str; long long counts=0 ,countsh=0 ,countshy=0 ; for (auto ch:str){ if (ch=='s' ) counts++; else if (ch=='h' ) countsh+=counts; else if (ch=='y' ) countshy+=countsh; } cout<<countshy<<endl; return 0 ; }
进阶版本
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 + 7 取模。
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int numDistinct (string s, string t) int n=s.length (),m=t.length (); vector<vector<int >> cache (n,vector <int >(m,-1 )); function<long long (int ,int )> dfs=[&](int i,int j)->long long { if (j<0 ) return 1 ; if (i<0 ) return 0 ; int & res=cache[i][j]; if (res!=-1 ){ return res; } if (s[i]==t[j]){ return res=dfs (i-1 ,j-1 )+dfs (i-1 ,j); } return res=dfs (i-1 ,j); }; return dfs (n-1 ,m-1 ); } };
游游有 n个苹果, m个桃子。她可以把2个苹果和1个桃子组成价值 a元的一号水果大礼包,
输入描述:
1 2 四个正整数 n,m,a,b,用空格隔开。分别代表苹果的数量、桃子的数量、一号大礼包价值、二号大礼包价值。 1≤n,m,a,b≤10^6
输出描述:
贪心算法
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <iostream> using namespace std;int main () long long n,m,a,b; cin>>n>>m>>a>>b; long long max_value=0 ; for (int i=0 ;i<=n/2 ;i++){ if (i<=n/2 &&i<=m){ int left_n=n-2 *i; int left_m=m-i; int j=min (left_n,left_m/2 ); max_value=max (max_value,i*a+j*b); } } cout<<max_value<<endl; return 0 ; }
请你实现一个简单的字符串替换函数。原串中需要替换的占位符为”%s”,请按照参数列表的顺序一一替换占位符。若参数列表的字符数大于占位符个数。则将剩下的参数字符添加到字符串的结尾。
给定一个字符串A,同时给定它的长度n及参数字符数组arg,请返回替换后的字符串。保证参数个数大于等于占位符个数。保证原串由大小写英文字母组成,同时长度小于等于500。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class StringFormat {public : string formatString (string A, int n, vector<char > arg, int m) { size_t pos=0 ; size_t paramindex=0 ; while ((pos=A.find ("%s" ,pos))!=string::npos){ if (paramindex<arg.size ()){ string tmp=string (1 ,arg[paramindex++]); A.replace (pos,2 ,tmp); pos++; }else { break ; } } while (paramindex<arg.size ()){ A+=arg[paramindex++]; } return A; } };
描述
洗牌在生活中十分常见,现在需要写一个程序模拟洗牌的过程。 现在需要洗2n张牌,从上到下依次是第1张,第2张,第3张一直到第2n张。
输入描述:
第一行一个数T(T ≤ 100),表示数据组数。对于每组数据,第一行两个数n,k(1 ≤ n,k ≤ 100),接下来有2n行个数a1,a2,…,a2n(1 ≤ ai ≤ 1000000000)。表示原始牌组从上到下的序列。
输出描述:
对于每组数据,输出一行,最终的序列。数字之间用空格隔开,不要在行末输出多余的空格。
思考:当前位置 当前位置+1
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <iostream> #include <vector> using namespace std;int main () int T; cin >> T; while (T--) { int n, k; cin >> n >> k; vector<int > cache (2 * n) ; for (int i=0 ;i<2 *n;i++){ cin>>cache[i]; } for (int j = 0 ; j < k; j++) { vector<int > tmp (cache.begin(), cache.end()) ; for (int m=0 ;m<n;m++){ cache[2 *m]=tmp[m]; cache[2 *m+1 ]=tmp[m+n]; } } for (auto x:cache){ cout<<x <<" " ; } cout<<endl; } return 0 ; }
题目描述
dd被困在了一个迷幻森林,现在她面前有一条凶险的大河,河中央有 n个神奇的浮块,浮块按 1∼n顺序标号,但两两并不相接,第
输入描述:
1 2 第一行一个数n(2≤n≤2000) 接下来一行n个数a[i](1≤|a[i]|≤2000)表示浮块上的数字
输出描述:
思路:
我们从第1个浮块开始,使用BFS逐层遍历每一个浮块。
对于每一个浮块,计算它可以传送到的其他浮块。
如果浮块上的数字是正数,我们可以向后传送,最多传送 a[i] 步。
如果浮块上的数字是负数,我们可以向前传送,最多传送 -a[i] 步。
传送的目标如果超过范围,按照题意处理。
BFS的过程中,每传送一次,记录时间 +1。
如果在BFS过程中到达第 n 个浮块,则输出对应的时间;如果BFS完成后仍未到达,则返回 -1。
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <iostream> #include <vector> #include <queue> #include <cstring> using namespace std;int main () int n; cin >> n; vector<int > a (n + 1 ) ; vector<int > dist (n + 1 , -1 ) ; for (int i = 1 ; i <= n; ++i) { cin >> a[i]; } queue<int > q; q.push (1 ); dist[1 ] = 0 ; while (!q.empty ()) { int i = q.front (); q.pop (); if (a[i] > 0 ) { for (int k = 1 ; k <= a[i] && i + k <= n; ++k) { int next = i + k; if (dist[next] == -1 ) { dist[next] = dist[i] + 1 ; q.push (next); } } } else { for (int k = 1 ; k <= -a[i]; ++k) { int next = i - k; if (next < 1 ) { next = 1 ; } if (dist[next] == -1 ) { dist[next] = dist[i] + 1 ; q.push (next); } } } } cout << dist[n] << endl; return 0 ; }
小红拿到了一个数字串(由’1’~’9’组成,不含’0’),她准备截取一段连续子串,使得该子串表示的正整数小于
输入描述:
1 2 第一行输入一个数字串,长度不超过200000。 第二行输入一个正整数 k。 1≤k≤10^9
输出描述:
双指针
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> #include <string> using namespace std;int main () string s; long long k; cin >> s >> k; int n = s.size (); int count = 0 ; for (int i = 0 ; i < n; ++i) { long long num = 0 ; for (int j = i; j < n; ++j) { num = num * 10 + (s[j] - '0' ); if (num < k) { count++; } else { break ; } } } cout << count << endl; return 0 ; }
题目描述
kotori最近在研究n皇后的问题。
所谓n皇后问题是这样的:一个n*n的地图,上面一共放n个皇后,保证任意两个皇后都不能互相攻击(每个皇后可以攻击同一行、同一列以及同一45度角斜线和135度角斜线上的所有其他皇后)。
kotori思考了很久都无法得出答案,整个人都变成琴梨了。她于是拿了一堆皇后在一个无穷大的棋盘上模拟,按照次序一共放了k个皇后。
但是,皇后的站位太复杂了,kotori甚至不知道是否存在两个皇后会互相攻击。于是她想问问聪明的你,在第i个皇后放置在棋盘上之后,是否存在两个皇后可以互相攻击?
输入描述:
1 2 3 4 5 第一行输入一个正整数k,代表总共放置的皇后的个数。(1<=k<=1e5) 接下来的k行,每行两个正整数xi和yi,代表每个皇后的坐标。(1<=xi,yi<=1e9) 之后输入一个正整数t,代表t次询问。(1<=t<=1e5) 接下来的t行,每行一个正整数i,代表询问第i个皇后放置后,是否存在互相攻击的情况。(1<=i<=k) 保证不存在两个皇后放置的位置相同。
输出描述:
1 共t行。每行对应当前的询问是否存在两个皇后可以互相攻击,若是则输出“Yes”,否则输出“No”
思考
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #include <unordered_map> using namespace std; int main() { int k; cin >> k; unordered_map<int, bool> row, col, diag1, diag2; int conflict_index = -1; for (int i = 1; i <= k; i++) { int x, y; cin >> x >> y; if (conflict_index == -1 && (row[x] || col[y] || diag1[x - y] || diag2[x + y])) { conflict_index = i; } row[x] = true; col[y] = true; diag1[x - y] = true; diag2[x + y] = true; } int t; cin >> t; while (t--) { int i; cin >> i; if (conflict_index != -1 && i >= conflict_index) { cout << "Yes" << endl; } else { cout << "No" << endl; } } return 0; }
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例
计算每个木桶左右壁的高度 选择最短的木板
解答
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int trap (vector<int >& height) int n=height.size (); int left=0 ,right=n-1 ; int pre_max=0 ,suf_max=0 ; int ans=0 ; while (left<right){ pre_max=max (pre_max,height[left]); suf_max=max (suf_max,height[right]); if (pre_max>suf_max){ ans+=suf_max-height[right--]; }else { ans+=pre_max-height[left++]; } } return ans; } };