优先队列 priority_queue
仿函数less 升序 -》大根堆
仿函数greater 降序 -》 小根堆
仿函数-》重载()
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
思路:
将所有的节点放到优先队列中 一个一个拿出来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
struct cmp {
bool operator()(ListNode* l1, ListNode* l2) {
return l1->val > l2->val;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
priority_queue<ListNode*, vector<ListNode*>, cmp> pq;
for (auto head : lists) {
if (head) {
pq.push(head);
}
}
ListNode* dummy =
new ListNode(0);
auto cur = dummy;
while (!pq.empty()) {
auto node = pq.top();
pq.pop();
if (node->next) {
pq.push(node->next);
}
cur->next = node;
cur = cur->next;
}
return dummy->next;
}
};
|
将一棵无穷大满二叉树的结点按根结点一层一层地从左往右编号,根结点编号为1。现给定a,b为两个结点。
设计一个算法,返回a、b最近的公共祖先的编号。注意其祖先也可能是结点本身。
测试样例:
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include <iostream>
using namespace std;
class LCA {
public:
int getLCA(int a, int b) {
while(a!=b){
if(a>b){
a/=2;
}else{
b/=2;
}
}
return a;
}
};
|
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历,
postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
实例
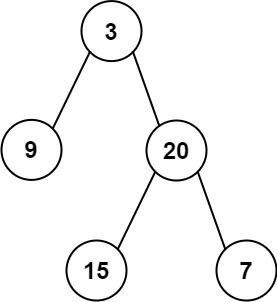
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
先根据后序遍历得知根节点 在中序遍历中的通过根节点分为两部分 左子树 右子树 递归即可
解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int n=inorder.size();
unordered_map<int,int> index;
for(int i=0;i<n;i++){
index[inorder[i]]=i;
}
function<TreeNode*(int,int,int,int)> dfs=[&](int in_l,int in_r,int post_l,int post_r)->TreeNode*{
if(post_l==post_r) return nullptr;
int left_size=index[postorder[post_r-1]]-in_l;
TreeNode* left=dfs(in_l,in_l+left_size,post_l,post_l+left_size);
TreeNode* right=dfs(in_l+left_size+1,in_r,post_l+left_size,post_r-1);
return new TreeNode(postorder[post_r-1],left,right);
};
return dfs(0,n,0,n);
}
};
|
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
根据二叉搜索树的性质
如果目标节点大于当前节点值,则去右子树中删除;
如果目标节点小于当前节点值,则去左子树中删除;
如果目标节点就是当前节点,分为以下三种情况:
其无左子:其右子顶替其位置,删除了该节点;
其无右子:其左子顶替其位置,删除了该节点;
其左右子节点都有:其左子树转移到其右子树的最左节点的左子树上,然后右子树顶替其位置,由此删除了该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key)
{
if (root == nullptr) return nullptr;
if (key > root->val) root->right = deleteNode(root->right, key);
else if (key < root->val) root->left = deleteNode(root->left, key);
else
{
if (! root->left) return root->right;
if (! root->right) return root->left;
TreeNode* node = root->right;
while (node->left)
node = node->left;
node->left = root->left;
root = root->right;
}
return root;
}
};
|




